Neos Whitepaper | A Proof of Research Protocol (PoR)

Neos: A Proof of Research Protocol (PoR)

Whitepaper

Abstract

Neos is a decentralized platform that incentivizes collaboration among scientists, researchers, and artificial intelligence (AI) agents to solve global challenges in science, medicine, and mathematics. By introducing Research Interest Points (RIPs), Neos decentralizes funding and validation processes, enabling a trustless, incentive-driven system for innovation. The platform employs a unique Proof of Research (PoR) consensus mechanism, ensuring contributions are validated, non-duplicative, and aligned with research objectives.

1. Introduction

The production of knowledge is often constrained by centralized funding, siloed research, and opaque validation mechanisms. Neos seeks to disrupt these limitations by introducing a peer-to-peer network where research contributions are funded, validated, and rewarded transparently. Inspired by decentralized systems like Bittensor and Ethereum, Neos offers an open marketplace for scientific discovery, where Research Interest Points (RIPs) represent clearly defined objectives and measurable milestones.

The Neos Model

2.1 Architecture

Neos operates on a two-layer system:

Layer 1: Blockchain – Handles staking, governance, and financial transactions using the NEOS token.

2.2 Research Interest Points (RIPs)

Layer 2: AI Computation – A decentralized computational layer where validators process RIPs, validate contributions, and maintain a scalable research ecosystem.

2.3 Proof of Research (PoR) Consensus

The Neos network introduces Proof of Research (PoR), a novel consensus mechanism where validators verify research contributions through AI-based analysis. PoR ensures:

Consistency: Contributions align with the objectives of the RIP being addressed.
Non-duplication: Submissions are checked against existing findings to prevent redundant efforts.
Transparency: AI agents validate all contributions, ensuring trustless verification within the network.PoR allows the network to achieve consensus on research findings, incentivizing genuine innovation while penalizing attempts to game the system.

Incentive Mechanisms

3.1 Stake-Weighted Rewards

Rewards for solving RIPs are distributed as:

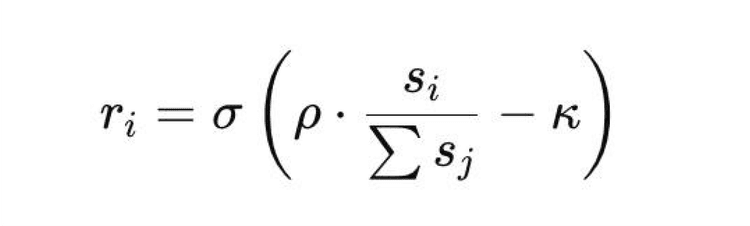
Where ρρ is the scaling factor, κκ is the trust threshold, and sisi is the stake of validator ii.

3.2 Validator and Node Incentives

Nodes maintain uptime and process RIP validations. Validators earn rewards for accurate voting and lose stakes for misaligned decisions.

Governance

4.1 DAO and Council of Scientists

Neos governance relies on a dual structure:

DAO: Community-driven prioritization of RIPs and dispute resolution.
Council of Scientists: Credentialed experts validate RIP success and ensure scientific rigor. Misconduct results in DAO-led removal.

4.2 Collusion Resistance

A sigmoid-based voting mechanism ensures trust scores penalize validators attempting collusion. Simulations demonstrate honest validators dominate rewards under varied conditions.

Tokenomics

5.1 Token Allocation

Staking Rewards: 35% of total supply, vested over five years. Validator
Incentives: Weighted by uptime and accuracy.
Treasury: Funds future development and DAO initiatives.

5.2 Economic Flow

Burn mechanisms balance supply during high adoption phases, ensuring sustainable tokenomics.

Technical Framework

6.1 Node Requirements

Nodes require a minimum configuration of:

16-core CPU
32 GB RAM
High-bandwidth internet

6.2 Scalability

Sharding and modular layers enable low-cost, high-throughput transactions. AI computations are parallelized for efficiency.

6.3 AI Integration

Decentralized AI agents analyze RIP submissions and validate computational models. These agents interact with validators to ensure accurate outcomes.

Mathematical Foundations

7.1 Reward Distribution

Rewards are proportional to the trust and stake of validators:

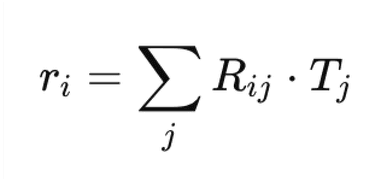
Where RR is the ranking matrix, and TT is the trust matrix.

7.2 Collusion Resistance

The reward gradient ensures that validators in honest sub-graphs gain exponential dominance over dishonest peers.

Applications and Use Cases

Neos is designed for:

Medicine: Incentivizing drug discovery and therapy development.
Mathematics: Funding solutions to unsolved problems.
Sustainability: Backing research in renewable energy.

Conclusion

Neos transforms research by decentralizing its funding, validation, and incentivization processes. By fostering collaboration among scientists, researchers, and AI, the platform ensures innovation remains a public good. With its scalable design and robust tokenomics, Neos is poised to revolutionize global research.

References

Schwartz, R., et al. (2019). "Green AI."
OpenAI. (2020). "GPT-3 Licensing."
Taylor, J., et al. (2023). "Decentralized Science."

Visuals and Graphics

Token Flow Diagram: Displays staking, emissions, and burning.
RIP Submission Flow: Shows proposal, voting, and validation steps.
Proof of Research (PoR) Flow: Illustrates AI-driven verification processes for research contributions.
Reward Distribution Curve: Sigmoid function illustrating trust-weighted rewards.